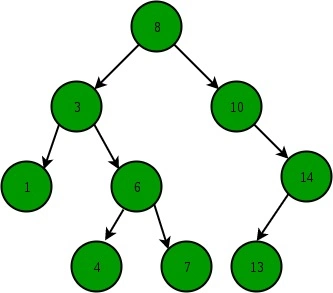
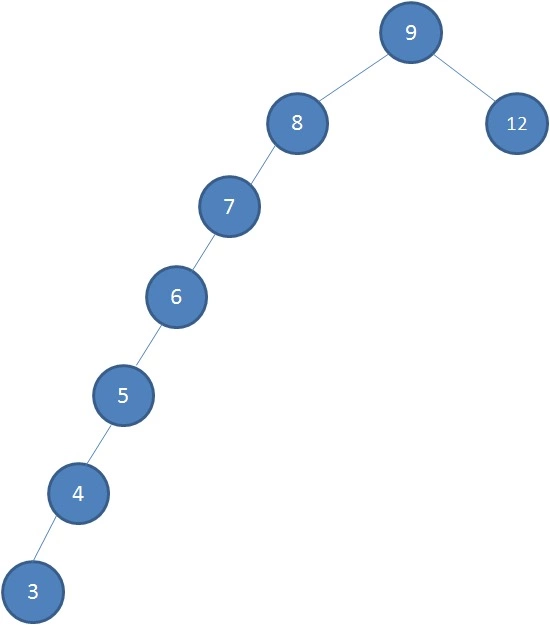
二叉查找树具有以下的特性:
某节点的左子树节点值仅包含小于该节点值
某节点的右子树节点值仅包含大于该节点值
左右子树每个也必须是二叉查找树
简单的讲:越小的放在越左边 。
你以为的二叉查找树 变态的二叉查找树 链表 ,查找节点的时间复杂度就会从O($ log_2^n $)退化成O(n) 。而根据我们在小学二年级就学过的[去除顶端优势],我们引入了红黑树,达到树的平衡。
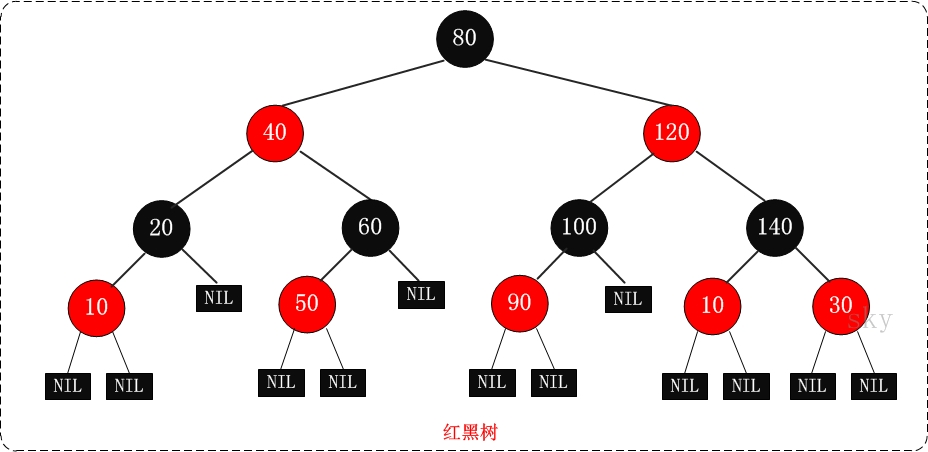
R-B Tree ,全称是Red-Black Tree,又称为“红黑树”,它一种特殊的二叉查找树 。红黑树的每个节点上都有存储位表示节点的颜色,可以是红(Red)或黑(Black)。
每个节点或者是黑色,或者是红色。(没啥用 )
根节点是黑色 。
每个叶子节点是黑色的 。如果一个节点是红色的,则它的子节点必须是黑色的。 从一个节点到该节点的子孙节点的所有路径上包含相同数目的黑节点。
第5点确保没有一条路径会比其他路径长出两倍。
示意图如下:
主要是用来储存有序的数据,时间复杂度为O(l o g 2 n log_2^n l o g 2 n TreeSet、TreeMap ,C++ STL中的set、map ,以及Linux中虚拟内存 的管理等。
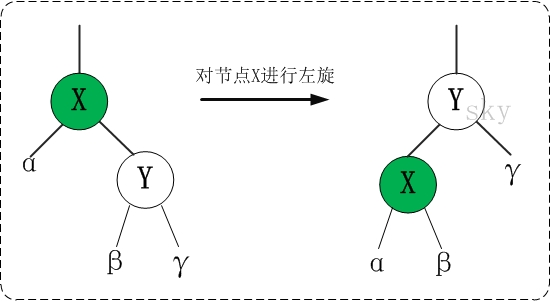
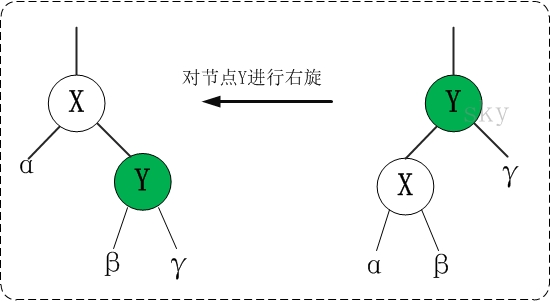
Recolor: 重新标记节点为黑色或红色Rotation: 旋转,达到树的平衡
当我们插入一个新的节点X时,要遵循如下公式:
将新插入的节点标记为红色
如果X是根节点,则标记为黑色
如果X的parent不是黑色,同时X也不是root:
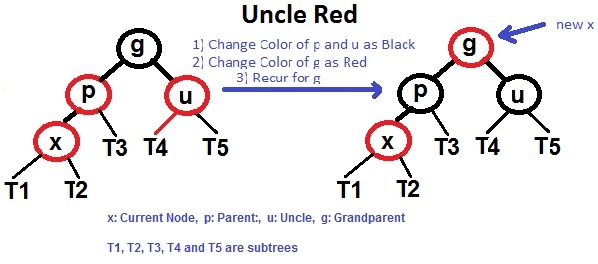
如果X的uncle是红色
将parent和uncle标记为黑色
将grand parent 标记为红色
让X的颜色和grand parent的颜色相同,重复2.3步骤
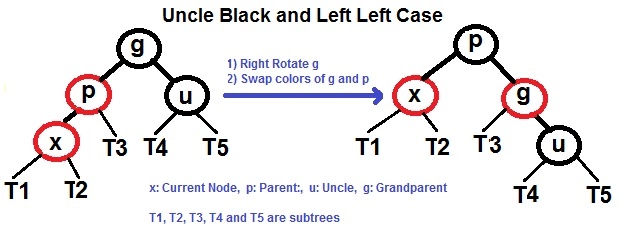
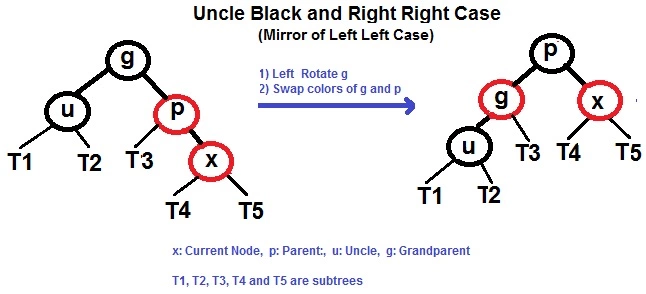
如果X的uncle是黑色
左左
左右
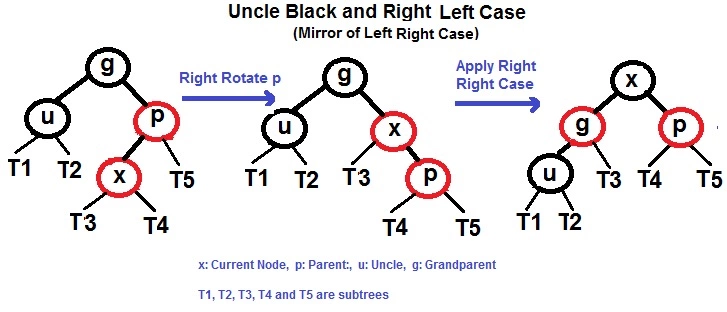
右右
右左
第一个左指的是parent节点是在grand parent的左边还是右边
跟着上面的公式走:
将新插入的 X 节点标记为红色
发现 X 的 parent § 同样为红色,这违反了红黑树的第三条规则「不能有两个连续相邻的红色节点」
发现 X 的 uncle (U) 同样为红色
将 P 和 U 标记为黑色
将 X 和 X 的 grand parent (G) 标记为相同的颜色,即红色,继续重复公式 2、3
发现 G 是根结点,标记为黑色
结束
p在g的左边,x在p的左边
右旋g
交换g和p的颜色
左旋p
变成左左了
左旋g
交换g和p的颜色
右旋p
变成右右了
插入 10,20,30,15 到一个空树中
向空树中第一次插入数字 10,肯定是 root 节点
root 节点标记成黑色
向树中插入新节点 20,标记为红色
20 > 10,并发现 10 没有叶子节点,将新节点 20 作为 10 的右孩子
向树中插入新节点 30,标记为红色
30 > 10,查找 10 的右子树,找到 20
30 > 20,继续查找 20 的右子树,发现 20 没有叶子节点,将值插在此处
30 和 20 节点都为红色,30 为右孩子,20 也为右孩子,触发了右右情况
通过一次旋转,提起 20 节点
20 节点是根结点,标记为黑色
向树中插入新节点 15,标记为红色
通过比对大小和判断是否有叶子节点,最终插值为 10 节点的右孩子
15 和 10 节点都为红色,15 的 uncle 节点 30 也为红色
按照公式,将 15 的 parent 10 和 uncle 30 更改为黑色
让 15 节点 grand parent 20 的颜色与 15 节点的颜色一样,变为红色
20 为根结点,将其改为黑色
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 #define RED 0 #define BLACK 1 typedef int Type;typedef struct RBTreeNode { unsigned char color; Type key; struct RBTreeNode *left ; struct RBTreeNode *right ; struct RBTreeNode *parent ; }Node, *RBTree; typedef struct rb_root { Node *node; }RBRoot;
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 #define RED 0 #define BLACK 1 typedef int Type;typedef struct RBTreeNode { unsigned char color; Type key; struct RBTreeNode *left ; struct RBTreeNode *right ; struct RBTreeNode *parent ; }Node, *RBTree; typedef struct rb_root { Node *node; }RBRoot;
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 static void rbtree_right_rotate (RBRoot *root, Node *y) Node *x = y->left; y->left = x->right; if (x->right != NULL ) x->right->parent = y; x->parent = y->parent; if (y->parent == NULL ) { root->node = x; } else { if (y == y->parent->right) y->parent->right = x; else y->parent->left = x; } x->right = y; y->parent = x; }
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 static void rbtree_insert (RBRoot *root, Node *node) Node *y = NULL ; Node *x = root->node; while (x != NULL ) { y = x; if (node->key < x->key) x = x->left; else x = x->right; } rb_parent(node) = y; if (y != NULL ) { if (node->key < y->key) y->left = node; else y->right = node; } else { root->node = node; } node->color = RED; rbtree_insert_fixup(root, node); }
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 static void rbtree_insert (RBRoot *root, Node *node) Node *y = NULL ; Node *x = root->node; while (x != NULL ) { y = x; if (node->key < x->key) x = x->left; else x = x->right; } rb_parent(node) = y; if (y != NULL ) { if (node->key < y->key) y->left = node; else y->right = node; } else { root->node = node; } node->color = RED; rbtree_insert_fixup(root, node); }
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 static void rbtree_insert (RBRoot *root, Node *node) Node *y = NULL ; Node *x = root->node; while (x != NULL ) { y = x; if (node->key < x->key) x = x->left; else x = x->right; } rb_parent(node) = y; if (y != NULL ) { if (node->key < y->key) y->left = node; else y->right = node; } else { root->node = node; } node->color = RED; rbtree_insert_fixup(root, node); }
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 static void rbtree_insert (RBRoot *root, Node *node) Node *y = NULL ; Node *x = root->node; while (x != NULL ) { y = x; if (node->key < x->key) x = x->left; else x = x->right; } rb_parent(node) = y; if (y != NULL ) { if (node->key < y->key) y->left = node; else y->right = node; } else { root->node = node; } node->color = RED; rbtree_insert_fixup(root, node); }
我打算在今后的板块中都增加一个Free Talk的环节,讲讲自己的感受。To be a better man!
参考链接:博客园 segment