LeetCode-BinarySearch

Free Talk

刚刚做到了 寻找重复数 ， 发现自己对 二分查找 还不是很熟悉，打算再做几题训练一下。

Finished Problem

搜索二维矩阵 II

240. 搜索二维矩阵 II

奇妙解法

class Solution {
    public boolean searchMatrix(int[][] matrix, int target) {
        // 思路肯定是 二分查找，不过要做一下变形
        // 矩阵相当是 二个维度的 普通二分查找
        // 二分查找的前提：数组必须是排序的
        // 简单的方法就是 对于矩阵的每一行进行二分查找 时间复杂度为 M Log N
        // 但是突然在题解中看到一种很赞的方法，直接放弃二分了
        // 思路：
        // 从右上角开始走
        // 如果当前值比 target 大，就往左走
        // 如果当前值比 target 小，就往下走
        // 秒啊！！！

        if(matrix.length == 0) return false;

        int m = matrix.length;
        int n = matrix[0].length;

        int i = 0;
        int j = n - 1;

        while(i < m && j >= 0){
            if(matrix[i][j] > target){
                j-- ;
            }else if(matrix[i][j] < target){
                i++ ;
            }else{
                return true;
            }
        }

        return false;

    }
}

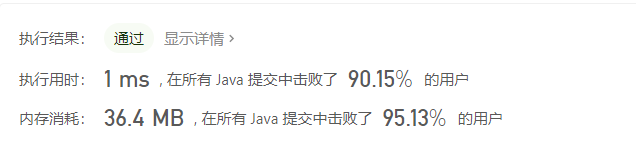
执行结果

最长上升子序列

300. 最长上升子序列

动态规划

class Solution {
    public int lengthOfLIS(int[] nums) {
        // 只要看到 Log N，第一反应就 二分查找
        // 但是没有想出解法
        // 看了一下题解中的动态规划
        // dp[i] 表示 第 i 个位置(含)前的最长升序子序列的长度

        if(nums.length == 0) return 0;

        int[] dp = new int[nums.length];
        // 初始化为 1
        Arrays.fill(dp, 1);
        int res = 0;

        for(int i = 0; i < nums.length ; i ++ ){
            for(int j = 0; j < i; j ++ ){
                if(nums[j] < nums[i]) dp[i] = Math.max(dp[i], dp[j] + 1);
            }
            res = Math.max(dp[i], res);
        }

        return res;
    }
}

执行结果

动态规划+二分查找

class Solution {
    public int lengthOfLIS(int[] nums) {
        // 动态规划 + 二分查找
        // 看题解看了半个小时，才想明白，吃完午饭再写
        // 算法的核心是构建一个 tails 数组，用来存放最长升序子串

        if(nums.length == 0) return 0;

        int[] tails = new int[nums.length];
        int res = 0;
        for(int num : nums){
            int i = 0, j = res;
            // 这里的目的是将当前数组的值，与 tails 数组中的值做比较，用到了二分查找
            while(i < j){
                int m = (i + j) / 2;
                if(num > tails[m]) i = m + 1;
                else j = m;
            }
            tails[i] = num;
            // j == res, 意味要添加入 tails 数组中的这个值，是可以放入上升子序列的末尾的
            if(j == res) res++;
        }

        return res;
    }
}

执行结果

完结撒花