LeetCode-DynamicProgramming

Free Talk

终于轮到 LeetCode 的大头了， 动态规划应该是占据了算法题的半壁江山，我们废话不多说，直接上代码。

Talk is cheap, Show me your Code!

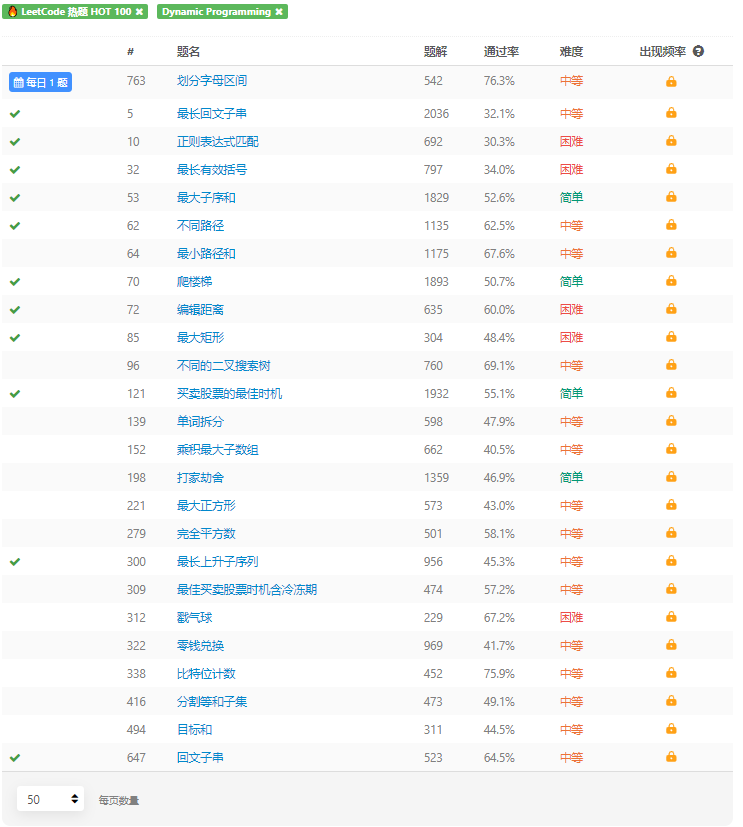
Finished Problem

最小路径和

64. 最小路径和

动态规划

class Solution {
    public int minPathSum(int[][] grid) {
        // 思路当然是动态规划啦
        // 动态规划的核心，在于构建动态方程
        // 路径的长度为 M + N - 1
        // dp[m][n] = Math.min((dp[m - 1][n] + grid[m][n]),dp[m][n - 1] + grid[m][n])
        if(grid.length == 0) return 0;

        int m = grid.length;
        int n = grid[0].length;

        int[][] dp = new int[m][n];
    
        // 第一次写没有考虑到边界问题
        // 其实还可以不用 dp 矩阵存放，直接在源矩阵上修改即可
        for(int i = 0; i < m; i ++ ){
            for(int j = 0; j < n ; j ++){
                if(i == 0 && j == 0) dp[0][0] = grid[0][0];
                else if(i == 0 && j != 0) dp[i][j] = dp[i][j - 1] + grid[i][j];
                else if(j == 0 && i != 0) dp[i][j] = dp[i - 1][j] + grid[i][j];
                else dp[i][j] = Math.min(dp[i - 1][j],dp[i][j - 1]) + grid[i][j];
            }
        }
        return dp[m - 1][n - 1];
    }
}

执行结果

刷完这题，终于把 LeetCode 刷到了 50 题，总算是入门了，开心！！！

不同的二叉搜索树

96. 不同的二叉搜索树

二叉搜索树

二叉查找树（BST：Binary Search Tree）是一种特殊的二叉树，它改善了二叉树节点查找的效率。二叉查找树有以下性质：

对于任意一个节点 n，

• 其左子树（left subtree）下的每个后代节点（descendant node）的值都小于节点 n 的值；
• 其右子树（right subtree）下的每个后代节点的值都大于节点 n 的值。

所谓节点 n 的子树，可以将其看作是以节点 n 为根节点的树。子树的所有节点都是节点 n 的后代，而子树的根则是节点 n 本身。

Reference：https://www.cnblogs.com/gaochundong/p/binary_search_tree.html

动态规划

class Solution {
    public int numTrees(int n) {
        // 思路应该是动态规划
        // 但是我想不到 动态方程
        // 偷瞄了一眼题解
        // 假设二叉树为 n 个节点
        // G(n) 为节点为 n 的 二叉搜索树的数量
        // f(i) 为以节点 i 为根节点的 二叉搜索树的数量
        // G(n) = f(1) + f(2) + ··· + f(n)  
        // f(i) = G(i - 1) * G(n - i) 由二叉查找树的性质决定的
        // 因此 G(n) = G(0)*G(n - 1) + G(1)*G(n - 2) + ··· + G(n - 1)*G(0)
        
        if(n == 0) return 0;

        int[] dp = new int[n + 1];
        dp[0] = 1;
        dp[1] = 1;

        for(int i = 2; i < n + 1; i ++ ){
            for(int j = 1 ; j <= i ; j ++ ){
                // G(2) = G(0)*G(1) + G(1)*G(0)
                dp[i] += dp[j - 1]*dp[i - j];
            }
        }

        return dp[n];
    }
}

执行结果

单词拆封

139. 单词拆分

动态规划 + 哈希表

class Solution {

    HashMap<String, Boolean> map = new HashMap<>();

    public boolean wordBreak(String s, List<String> wordDict) {
        // 思路是动态规划
        // 首先是找到动态方程
        // 因为之前没有做过字符串的动态规划
        // 于是看了一下题解
        // dp[j] 为 前 j 个字符 是否 可以拆解为字典中出现的单词
        // 因此就是遍历判定 前 i 个字符是否可以拆解，且 j - i 中的字符是否在字典中出现
        // dp[j] = dp[i] && check(j - i) 

        if(s.length() == 0) return false;
        
        boolean[] dp = new boolean[s.length() + 1];
        // 初始化
        dp[0] = true;

        // 将字典中的单词存入哈希表，方便查询
        for(String word: wordDict){
            map.put(word,true);
        } 
        
        for(int j = 1; j <=s.length(); j ++ ){
            for(int i = j - 1; i >= 0; i -- ){
                // 从 i 开始(含)，到 j 结束的(不含)的字符串
                dp[j] = dp[i] && check(s.substring(i, j));
                if(dp[j]) break;
            }
        }

        return dp[s.length()];
    }

    public boolean check(String word){
        return map.getOrDefault(word,false);
    }
}

执行结果

乘积最大子数组

失败解法

class Solution {
    public int maxProduct(int[] nums) {
        // 动态规划
        // if(dp[j - 1] * nums[j - 1] > dp[j - 1]) dp[j] = dp[j - 1] * nums[j - 1]; 
        // max = Math.max(max, dp[j]);
        // else dp[j] = 1; 
        // 一直没有提交成功，应该是方程有问题
       
       int[] dp = new int[nums.length + 1];
       dp[0] = 1;
       int max = Integer.MIN_VALUE;

       for(int j = 1 ; j <= nums.length ; j ++ ){
           if(j == 1){
               dp[j] = nums[j - 1];
               max = dp[j];
               continue;
           }
           if(dp[j - 1] * nums[j - 1] > dp[j - 1] || nums[j - 1] > dp[j - 1]){
               dp[j] = Math.max(dp[j - 1] * nums[j - 1], nums[j - 1]);
               max = Math.max(max, dp[j]);
           }
           else dp[j] = 1;
       }

       return max;
    } 
}

动态规划 + 维护最小值

class Solution {
    public int maxProduct(int[] nums) {
        // 看了一下题解
        // 真的叹为观止
        // 其中维护最小值的思路相当重要

        int max = Integer.MIN_VALUE, imax = 1, imin = 1;
        for(int num : nums){
            if(num < 0){
                int tmp = imax;
                imax = imin;
                imin = tmp;
            }

            imax = Math.max(imax * num, num);
            imin = Math.min(imin * num, num);

            max = Math.max(max, imax);
        }

        return max;
    }
}

执行结果

打家劫舍

198. 打家劫舍

动态规划 + 数组

class Solution {
    public int rob(int[] nums) {
        // 动态规划
        // 太简单了
        // dp[j] = Math.max(dp[j - 2] + nums[j - 1], dp[j - 1])

        if(nums.length == 0) return 0;

        int[] dp = new int[nums.length + 1];
        dp[0] = 0;
        dp[1] = nums[0];

        for(int j = 2; j <= nums.length ; j ++ ){
            dp[j] = Math.max(dp[j - 2] + nums[j - 1], dp[j - 1]);
        }

        return dp[nums.length];
    }
}

执行结果

最大正方形

221. 最大正方形

四个角

class Solution {
    public int maximalSquare(char[][] matrix) {
        // 动态规划
        // 我总觉得这题应该做过类似的，是最大矩形
        // 这题是最大正方形，应该不能当时的柱形图的思路
        // dp[i][j] 为 以 (i, j)为右下角的只包含 1 的正方形的面积
        // dp[i][j] = Math.min(dp[i - 1][j], dp[i][j - 1], dp[i - 1][j - 1]) + 1
        
        if(matrix == null || matrix.length == 0) return 0;

        int[][] dp = new int[matrix.length][matrix[0].length];
        int maxSide = 0;

        for(int i = 0; i < matrix.length ; i ++ ){
            for(int j = 0; j < matrix[0].length ; j ++ ){
                if(matrix[i][j] =='1'){
                    // 做边界处理
                    if(i == 0 || j == 0){
                        dp[i][j] = 1;
                    }else{
                        dp[i][j] = Math.min(dp[i - 1][j], Math.min(dp[i - 1][j - 1], dp[i][j - 1])) + 1;
                    }
                    maxSide = Math.max(maxSide, dp[i][j]);
                }
            }
        }

        return maxSide * maxSide;
    }
}

执行结果

完全平方数

279. 完全平方数

转换思维 + 平方和

class Solution {
    public int numSquares(int n) {
        // 动态规划
        // 这题应该要转换思路
        // 用每个数的平方来凑出这个数
        // dp[i] 表示 i 可以用多少个完全平方和凑出
        // dp[i] = Min(dp[i], dp[i - j * j] + 1)

        int[] dp = new int[n + 1];
        for(int i = 1; i <= n ; i ++ ){
            // 最大值为 1 累加和
            dp[i] = i;
            for(int j = 1; i - j * j >= 0; j ++ ){
                dp[i] = Math.min(dp[i], dp[i - j * j] + 1);
            }
        }

        return dp[n];
    }
}

执行结果

最佳买卖股票时机含冷冻期

309. 最佳买卖股票时机含冷冻期

定义三个状态

class Solution {
    public int maxProfit(int[] prices) {
        // 动态规划
        // 我发现找出动态方程真的太难了
        // 自己没有根据具体的情况定义动态方程的数组
        // dp[prices.length][3]
        // 0 表示已持有
        // 1 表示可购买
        // 2 表示不可购买

        if(prices.length == 0 || prices.length < 2) return 0;
        int[][] dp = new int[prices.length][3];
        int maxSales = 0;

        dp[0][0] = - prices[0];
        for(int i = 1; i < prices.length; i ++ ){
            dp[i][0] = Math.max(dp[i - 1][0], dp[i - 1][1] - prices[i]);
            dp[i][1] = Math.max(dp[i - 1][2], dp[i - 1][1]);
            dp[i][2] = dp[i - 1][0] + prices[i];
        }

        maxSales = Math.max(dp[prices.length - 1][1],dp[prices.length - 1][2]);

        return maxSales;
    }
}

执行结果

戳气球

312. 戳气球

区间定义 + 动态规划

class Solution {

    public int maxCoins(int[] nums) {
        // 动态规划
        // 自己瞎想了半天，发现逻辑都是错误的
        // 看了题解，发现动态规划的核心在于 子问题必须独立
        // 同时求解时 状态转移方程 所依赖的状态必须提前求出来 这个由遍历方式来解决

        int n = nums.length;
        int[] points = new int[n + 2];
        points[0] = points[n + 1] = 1;

        for(int i = 1; i < n + 1; i ++){
            points[i] = nums[i - 1];
        }

        int[][] dp = new int[n + 2][n + 2];

        // 从下往上遍历
        for(int i = n; i >= 0; i -- ){
            // 从左往右遍历
            for(int j = i + 1; j < n + 2; j ++ ){
                // dp[i][j]
                for(int k = i + 1; k < j; k ++){
                    dp[i][j] = Math.max(
                        dp[i][j],
                        // 这一个方程是精髓，最后戳破的是 k
                        dp[i][k] + dp[k][j] + points[i]*points[k]*points[j]
                    );
                }
            }
        }

        return dp[0][n + 1];    
    }
}

执行结果

零钱兑换

322. 零钱兑换

遍历数组 + 动态规划

class Solution {
    public int coinChange(int[] coins, int amount) {
        // 刚刚看完递归算法的解题框架，来小试牛刀了
        // dp[n] 表示凑出 n 元 所需要的最少硬币数
        // dp[i] = Math.min(dp[i - coins[j]] + 1 ,dp[i])

        int[] dp = new int[amount + 1];
        // 这步是给出一个 不可能 的值，用来后面比较与最后的返回值
        Arrays.fill(dp,amount + 1);
        dp[0] = 0;

        for(int i = 1; i < amount + 1; i ++ ){
            for(int coin: coins){
                if(i - coin < 0) continue;
                dp[i] = Math.min(dp[i - coin] + 1, dp[i]);
            }
        }
        return (dp[amount] == amount + 1 )? -1: dp[amount]; 
    }
}

执行结果

比特位计数

338. 比特位计数

奇偶判断 + 动态规划

class Solution {
    public int[] countBits(int num) {

        // if(i % 2 == 1) dp[i] = dp[i - 1] + 1;
        // else dp[i] = 1;

        int[] dp = new int[num + 1];
        dp[0] = 0;

       for(int i = 1 ; i < num + 1; i ++ ){
           if(i % 2 == 1) dp[i] = dp[i - 1] + 1;
           // 这边为偶数的情况，自己没有考虑好
           else dp[i] = dp[i / 2];
           }
           return dp;
    }
}

执行结果

分割等和子集

416. 分割等和子集

0-1 背包问题

class Solution {
    public boolean canPartition(int[] nums) {
        // 最简单的最傻逼的方法就是生成所有的子集，然后比较子集是否相等
        // 计算一下 数组中所有元素的和
        // 找子集 就相等于找 子集中是否存在两个和 为 sum/2 的子集
        // 看了题解的 0-1 背包问题

        if(nums.length == 0) return false;

        int sum = 0;
        for(int num: nums){
            sum += num;
        }

        if(sum % 2 == 1) return false;
        int target = sum / 2;
        boolean[][] dp = new boolean[nums.length][target + 1];

        if(nums[0] < target){
            dp[0][nums[0]] = true;
        }

        for(int i = 1; i < nums.length ; i ++ ){
            for(int j = 0; j < target + 1; j ++ ){
                dp[i][j] = dp[i - 1][j];

                if(nums[i] == j){
                    dp[i][j] = true;
                    continue;
                }
                if(nums[i] < j){
                    dp[i][j] = dp[i - 1][j] || dp[i - 1][j - nums[i]];
                }
            }
        }

        return dp[nums.length - 1][target];
    }
}

执行结果

目标和

494. 目标和

带加减的背包问题

class Solution {
    public int findTargetSumWays(int[] nums, int S) {
      // 难啊，自己想了半天，发现要考虑加减真的难
      // 在背包问题的基础上，通过增加数组的范围，解决索引为负的问题

      int sum = 0;
      for(int num: nums){
          sum += num;
      }

      if(Math.abs(sum) < Math.abs(S)) return 0;

      int t = 2*sum + 1;
      int[][] dp = new int[nums.length][t];

      if(nums[0] == 0){
          dp[0][sum] = 2;
      }else{
          dp[0][sum - nums[0]] = 1;
          dp[0][sum + nums[0]] = 1;
      }

      for(int i = 1; i < nums.length ; i ++){
          for(int j = 0; j < t ; j ++){
              int left = (j - nums[i]) >= 0 ? j - nums[i] : 0;
              int right = (j + nums[i]) < t ? j + nums[i] : 0;
              dp[i][j] = dp[i - 1][left] + dp[i - 1][right];
          }
      }

      return dp[nums.length - 1][S + sum];
    }
}

执行结果

完结撒花

其实我挺失落的，因为动态规划的问题，属于那种刷着很爽，但是真的太难想出状态转移方程了。真的是不看题解一筹莫展，看了之后豁然开朗。打算晚上写一篇动态规划的总结方法，不能让这么多题白刷。

定义数组元素的含义

找出状态转移方程

给出初始值

优化

参考链接