Free Talk

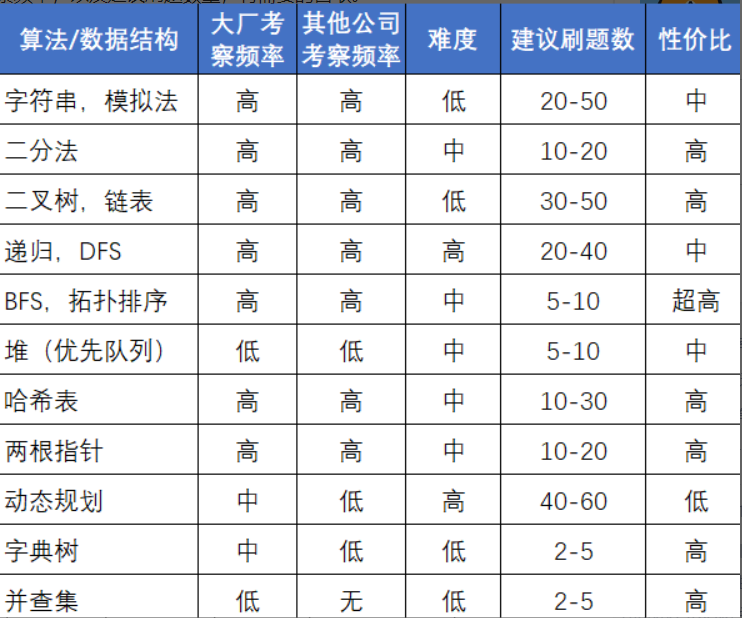
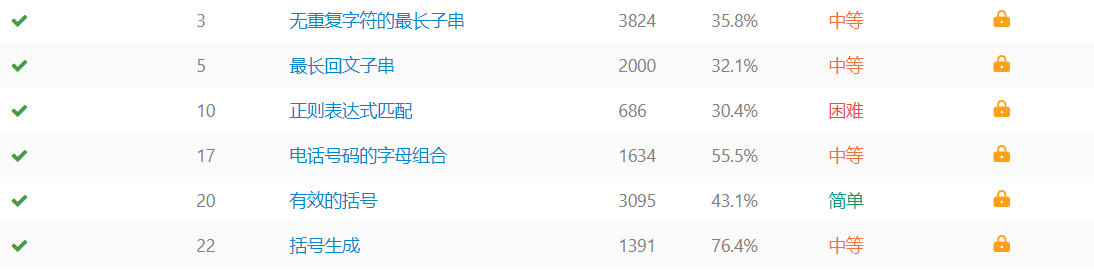
最近一直刷 Array Tags，有点无聊了，找了一份常见算法数组题图片，打算开启 String Tags 新篇章了。

Finished Problem

最长有效括号

错误解法

class Solution {
    public int longestValidParentheses(String s) {

        // 方法一：使用一个栈来存放左右括号
        // 遇到左括号就进行入栈
        // 遇到右括号就出栈
        // 再设置一个常量记录出栈的数量

        Stack<Character> st = new Stack<Character>();
        int number = 0;
        for(int i = 0; i < s.length(); i ++ ){
            char ch = s.charAt(i);
            if(ch == '('){
                st.push(ch);

                continue;
            }
            if(ch == ')'){
                if(!st.empty() && st.pop() == '('){
                    number ++;
                }
            } 
        }
        return number * 2;
    }
}

我看到这题是困难问题，先紧张了一下，后面马上就想出了上面的思路，一开始信心慢慢，顺利通过了测试，但是提交的时候就一直过不去了。去看了一下题解，发现自己理解错题目意思了。是计算最长子串 ‘()’ 长度，而不是我理解的合理的字符串长度。

正确解法

class Solution {
    public int longestValidParentheses(String s) {
        // 正确方法：
        // 栈用来存放字符的索引
        // 思路：
        // 将栈初始化，存入-1
        // 将左字符串的索引入栈
        // 当出现右字符串时，执行出栈，进行判断
        // ① 栈内有左字符串的索引，则更新 最长子串长度为 i - Stack.peek()
        // ② 栈内没有左字符串的索引，则将改右字符串的索引入栈，保持栈顶的元素为 最后一个未匹配的右字符串位置

        int maxLength = 0;
        Stack<Integer> st = new Stack<Integer>();
        st.push(-1);

        for(int i = 0; i < s.length(); i ++ ){
            if(s.charAt(i) == '('){
                st.push(i);
            }else{
                st.pop();
                if(st.empty()){
                    st.push(i);
                }
                else{
                    maxLength = Math.max(maxLength, i - st.peek());
                }
            }
        }

        return maxLength;
    }
}

执行结果

字母异位词分组

49. 字母异位词分组

排序数组

class Solution {
    public List<List<String>> groupAnagrams(String[] strs) {
        // 没有什么清晰的思路
        // 看了官方题解，里面的排序思路还是比较好理解的
        // 将字符串的数组里的每个字符串排序后
        // 作为Key 存入 HashMap, Value 为 排序相同的字符串 List
        // 需要去熟悉一下 HashMAp 的 API
        
        if(strs.length == 0) return new ArrayList();
        Map<String, List> ans = new HashMap<String, List>();
        for(String s: strs){
            char[] ch = s.toCharArray();
            Arrays.sort(ch);
            String key = String.valueOf(ch);
            if(!ans.containsKey(key)) ans.put(key, new ArrayList());
            ans.get(key).add(s);
        }

        return new ArrayList(ans.values());
    }
}

执行结果

常用API

获取 String 数组长度：String.length;
字符串转换为字符数组：char[] = String.toCharArray();
字符数组转为字符串：String = String.valueOf( char[] ) ;
HashMap
1. Put：HashMap.put(key, value);
2. Get：HashMap.get(key) return value;
3. Key 的存在：HashMap.containsKey(key);

编辑距离

72. 编辑距离

动态规划

class Solution {
    public int minDistance(String word1, String word2) {

        // 又到了特别的尴尬的没有思路时刻
        // 刚刚看了官方题解
        // 动态规划
        // 其中将操作替换的思想特别新颖
        // A B 字符串总共有 6 种操作
        // 但是可以等效替换为 3 种
        // A 插入一个字符 == B 删除一个字符
        // B 插入一个字符 == A 删除一个字符
        // A 替换一个字符 == B 替换一个字符
        // 利用二维数组来存放[i][j] 来表示 字符串 A 的前 i 个字符和 字符串 B 的前 j 个字符需要匹配的最少操作数
        // 考虑四个具体问题
        // left = [i - 1][j] + 1;
        // down = [i][j] + 1;
        // left_down = {
        // 最后一个字符相同：[i - 1][j - 1];
        // 最后一个字符不同：[i - 1][j - 1] + 1; 做一次替换就好
        // }
        // [i][j] = Math.min{left, down, left_down };
        // 边界初始化处理：[i][0] = i, [0][j] = j;


        int m = word1.length();
        int n = word2.length();
       

        int [][] dp = new int[m + 1][n + 1];

        // 判空
        if(m * n == 0){
            // m 或 n 为零， 返回非空字符串长度
            return m + n;
        }
        
        // 初始化边界值
        for(int i = 0; i < m + 1; i ++ ) dp[i][0] = i;
        for(int j = 0; j < n + 1; j ++ ) dp[0][j] = j;

        // 计算最小操作数
        for(int i = 1; i < m + 1; i ++ ){
            for(int j = 1; j < n + 1; j ++){
                int left = dp[i - 1][j] + 1;
                int down = dp[i][j - 1] + 1;
                int left_down = dp[i - 1][j - 1];
                if(word1.charAt(i - 1) != word2.charAt(j - 1)) {
                    left_down = dp[i - 1][j - 1] + 1;
                }
                dp[i][j] = Math.min(left, Math.min(down, left_down));      
            }
        }

        return dp[m][n];
    }
}

执行结果

回文子串

647. 回文子串

动态规划

class Solution {
    public int countSubstrings(String s) {
        //  为什么又没有思路
        //  看到一个动态规划的题解，觉得很好接受
        //  思想是用一个二维数组[i][j] 表示字符串 i 到 j 之间的子串是回文子串
        //  动态规划的思想：
        //  s[i] == s[j] 当前要加入的两边字符相等
        //  (j - i < 2) 里面的子串个数是小于2的，即只有一个或没有字符
        //  [i + 1][j - 1] i + 1 到 j - 1 之间的子串是回文子串
        // s[i] == s[j] && ((j - i < 2) || ([i + 1][j - 1]))

        int n = s.length();
        int count = 0;

        boolean [][] dp = new boolean [n][n];
		
        // 注意一下循环的条件，i 和 j 都是从 0 开始， i <= j
        for(int j = 0; j < n ; j ++ ){
            for(int i = 0; i <= j; i ++ ){
                if(s.charAt(i) == s.charAt(j) && (((j - i) < 2) || dp[i + 1][j - 1])){
                    dp[i][j] = true;
                    count ++;
                }
            }
        }

        return count;
    }
}

执行结果

覆盖最小子串

76. 最小覆盖子串

class Solution {
    public String minWindow(String s, String t) {
        // 发现字符串的题 很多情况都是找子串问题
        // 问题：如何从字符串中找到目标子串
        // 滑动窗口
        // 方法：整型数组存放 Char， Char 的 int 值范围为 0 ~ 127
        // 利用数组 window 存放窗口中字符个数
        // 利用数组 need 存放匹配子串中需要的字符个数

        // 如果字符串为空，或者长度小于需要匹配的长度
        if(s.length() == 0 || t.length() == 0 || s.length() < t.length()){
            return "";
        }

        int[] need = new int[128];
        int[] window = new int[128];

        // 窗口中已经匹配的字符个数
        int count = 0;
        int left = 0;
        int right = 0;
        int minLength = s.length();
        String minString = "";

        // need 初始化
        for(int i = 0; i < t.length(); i ++ ){
            need[t.charAt(i)] ++;
        }

        while(right < s.length()){
            char ch = s.charAt(right);
            window[ch] ++;
            // 如果需要该字符，并且已有窗口内的字符个数 小于需要的字符个数
            if(need[ch] > 0 && need[ch] >= window[ch]){
                count ++;
            }

            // 当需要的字符都已经包含在窗口中后，开始收缩 left
            while(count == t.length()){
                ch = s.charAt(left);
                // 当需要删除的字符，是必须留在窗口内时
                if(need[ch] > 0 && need[ch] == window[ch]){
                    count --;
                }
                // 这边需要取 = ，因为可能一开始两个字符串就是匹配的，如 a , a return a
                if(right - left + 1 <= minLength){
                    minLength = right - left + 1;
                    minString = s.substring(left, right + 1);
                }
                window[ch] --;
                left ++;
            }
            right ++;
        }

        return minString;
    }
}